Now, let’s be clear about one thing: I couldn’t care less about the Academy Awards in general, or this year’s Best Oscar nominees in particular. I haven’t yet enjoyed the pleasure of seeing any of the movies in question, and due to Jessica Alba’s unfortunate absence from their respective casts, I am rather unlikely to see any of them, period. However, I do care a bit about economics, and love a good controversy. It seems as though America is all atwitter about why Brokeback Mountain lost to Crash, despite being both critically and commercially more successful.

I am confident none of the analysts will hit upon the true reason: the Academy’s method of voting is flawed. (Look, this blog is going to get a bit serious now. If you don’t like the lack of Texas Hold ‘Em and Paris Hilton coverage, go get your own bloody blog.)

Take the following example of ten voters, which could be analogous to deciles of voting groups within the entire population of Academy voters:
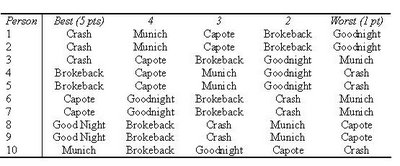In the above example, each row represents a voter’s preferences – reading from left to right are rankings from favourite to least-liked. In this example, using the Academy’s method of voting, Crash wins best picture with 30% of the vote, as the other votes are split in a 3-way tie (with three films each receiving a 20% share and Munich bringing up the rear with 10%).

However, upon examination of this data: 7 out of 10 voters actually think that Brokeback Mountain is a better picture than Crash. In fact, 7 out of 10 voters even think that Good Night, and Good Luck is a better picture than Crash! But this is madness! How does Crash still win if a clear majority think it to be inferior to two other movies on the list?

Well, our methods of voting do not always successfully translate the preferences of our populations. Such problems of voting structures have been closely examined by economists and mathematicians since at least the 18th century. At that time, a mathematician named J. C. Borda, despite the obvious handicap of being French, hit upon a neat solution: assign, via a system of points, a score to each preference rank for each voter. This is the method the Associated Press uses to rank college basketball teams, and it works rather well. Using the Borda method, assigning the first choice 5 points, the least favourite 1 point, and so forth, the following tally occurs:

Brokeback 35
Capote 32
Good Night 29
Crash 28
Munich 26

Under this system, Brokeback Mountain edges out Capote to take the Oscar, and Crash does not even crack the top three. As University of California Professor Donald G. Saari has pointed out, the Borda count method is now believed to be among the most efficient at “aggregating social preferences”, in the jargon.

But is my example relevant, or even remotely realistic? In a five-horse race, with differences of opinion amongst the voters (“heterogeneous preferences”) this type of thing most likely happens all the time. I once had a professor who told me to ignore every Academy Award result because they are probably wrong more than half the time (wrong in that the result inaccurately captures the preferences of the voters).

So, the real scandal here isn’t that Brokeback lost, but that the Academy is holding on to an archaic voting system that has little chance of capturing its members’ preferences. But remember, these are the same people who greenlighted and financed “Gigli”, so they deserve pretty much what they get.

Phonies.